Adversarial Search

Created in December 06, 2023

2023   ·   search   AI   ·   artificial-intelligence

双人零和博弈

双人零和博弈 (two-player zero-sum game) 是指两个玩家的收益之和为零的博弈，是一种确定性的、双人、轮流、完全可观测的零和博弈；零和意味着一方的收益等于另一方的损失，即一方的收益为正，另一方的收益为负，两者之和为零。

在博弈的形式化定义中，通常用移动 (move) 来代替动作 (action)，用局面 (position) 来代替状态 (state)，用玩家 (player) 来代替代理 (agent)。形式化定义一般需要以下几个要素：

  • 初始状态 (initial state, \(S_0\))：博弈开始时的局面。
  • 终止状态 (terminal state, \(S_T\))：博弈结束时的局面。
  • Is_Terminal(\(S\))：判断局面 \(S\) 是否为终止状态。
  • To_Move(\(S\))：返回局面 \(S\) 中应该移动的玩家。
  • Actions(\(S\))：返回局面 \(S\) 中所有可能的移动。
  • Result(\(S\), \(a\))：返回局面 \(S\) 中玩家采取动作 \(a\) 后的局面。
  • Utility(\(S\), \(P\))：返回玩家 \(P\) 在局面 \(S\) 中的收益。
    • 当博弈只在两个玩家之间就行时，效用函数可以返回一个实数\(f\rightarrow \mathbb{R}\)，表示玩家\(P_1\)的收益，玩家\(P_2\)的收益为\(-\text{Utility}(S)\)，即玩家\(P_2\)的收益为玩家\(P_1\)的损失。
    • 当博弈在多个玩家之间进行时，效用函数可以返回一个向量\(f\rightarrow \mathbb{R}^n\)，表示每个玩家的收益。

博弈树 (game tree) 是一种树形结构，它的每个节点都是一个局面，每个节点的子节点都是该节点的所有可能移动的结果。博弈树的叶子节点是终止状态，博弈树的根节点是初始状态。博弈树的高度是博弈的回合数，博弈树的宽度是每个局面的可能移动数。

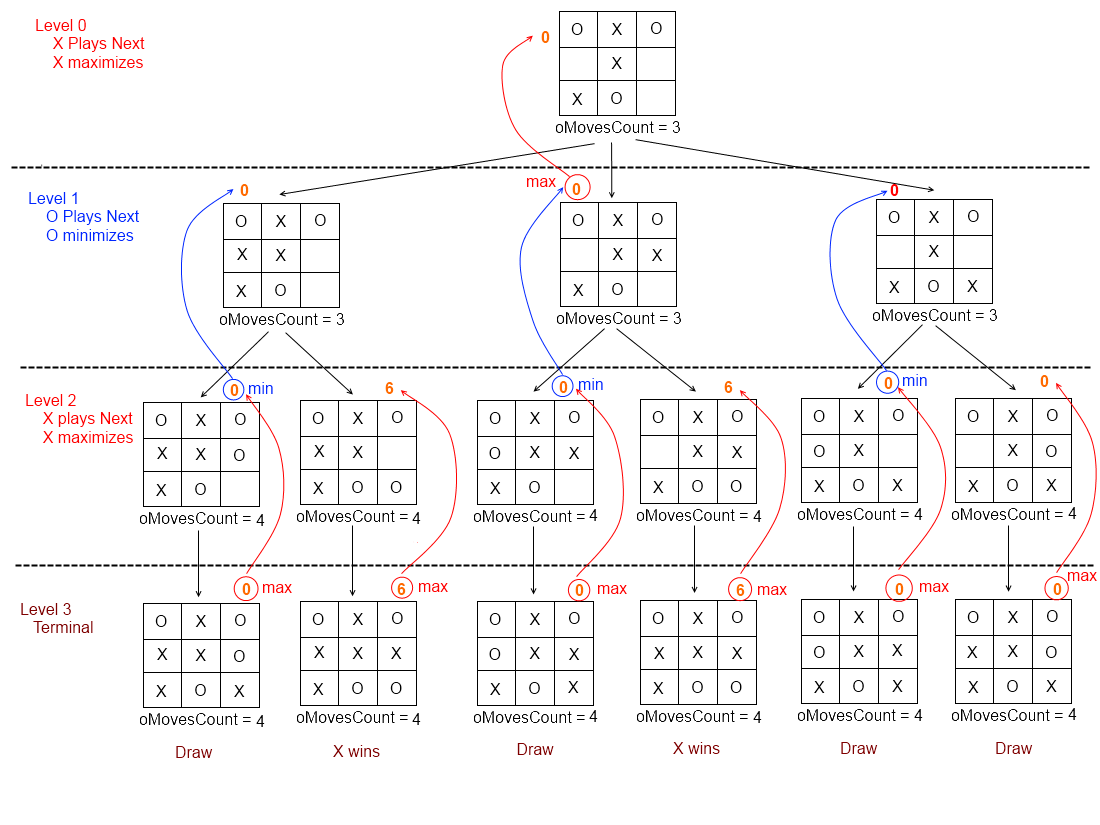
极小极大搜索

每个参与者都以最优策略行动，在每一步决策时都选择自身收益最大的动作，即

\[\max\limits_{a \in Actions(S)} \text{Utility}(Result(S, a), P)\]

极小极大化搜索是一种递归式的搜索算法，它的思想是在每一步决策时，假设对手会采取最优策略，然后选择自身收益最大的动作。在每一步决策时，都会递归地调用极小极大化搜索，直到博弈结束。



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

 
def Minimax_Search(state) -> action:
    player = To_Move(state) # 当前玩家
    value, action = Max_Value(state, player) # 极小极大化搜索
    return action # 返回最优动作 

def Max_Value(state, player: int) -> (value, action):
    if Is_Terminal(state): # 终止状态
        return Utility(state, player), None # 返回收益，动作为空
    value = -np.inf # 最大收益
    action = None # 最优动作
    for a in Actions(state): # 遍历所有可能的动作
        next_state = Result(state, a) # 采取动作后的局面
        next_player = To_Move(next_state) # 下一步的玩家
        next_value, _ = Max_Value(next_state, next_player) # 递归调用极小极大化搜索
        if next_value[player] > value: # 更新更大的收益和更优的动作
            value = next_value[player] # 更新最大收益
            action = a # 更新最优动作
    return value, action # 返回最大收益和最优动作

Alpha-Beta 剪枝

考虑博弈树中某一层的一个节点，若玩家在同层的节点或更上层的节点中有更好的选择，那么该节点将不再会被访问，因为玩家不会选择它。Alpha-Beta 剪枝算法就是利用这一思想，减少极小极大化搜索的节点访问次数。在极小极大化搜索的基础上，我们需要为每位玩家维护一个已知的最大收益列表，在搜索过程中，如果某个节点的最大收益小于已知的最大收益，那么该节点将不再会被访问。



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

 
def Alpha_Beta_Search(state) -> action:
    max_reached_value = [-np.inf] * num_players # 已知的最大收益列表
    player = To_Move(state) # 当前玩家
    value, action = Max_Value(state, player, max_reached_value) # 极小极大化搜索
    return action # 返回最优动作

def Max_Value(state, player: int, max_reached_value: list) -> (value, action):
    if Is_Terminal(state): # 终止状态
        return Utility(state, player), None # 返回收益，动作为空
    value = max_reached_value[player] # 已知的最大收益
    action = None # 最优动作
    for a in Actions(state): # 遍历所有可能的动作
        next_state = Result(state, a) # 采取动作后的局面
        next_player = To_Move(next_state) # 下一步的玩家
        next_value, _ = Max_Value(next_state, next_player, max_reached_value) # 递归调用极小极大化搜索
        if next_value[player] > value: # 更新更大的收益和更优的动作
            value = next_value[player] # 更新最大收益
            action = a # 更新最优动作
            max_reached_value[player] = value # 更新已知的最大收益
        else:
            break # 剪枝
    return value, action # 返回最大收益和最优动作

移动顺序

考虑两种极端的\(\alpha\)-\(\beta\)剪枝情况:

  1. 某一深度下第一个遍历的节点是最优的，那么剩下的节点都会被剪枝。
  2. 某一深度下所有节点的效用值依次增加，那么所有节点都不会被剪枝。

这说明遍历顺序会影响\(\alpha\)-\(\beta\)剪枝的效果，因此我们需要对节点进行排序，使得效用值更大的节点先被遍历，效用值更小的节点后被遍历。

当节点效用未知时，排序显然是无法实现的；因此移动顺序适用于非终止节点可评价的搜索情况，如存在评价函数或迭代加深搜索，根据先前记录的节点价值就可以对节点进行排序。

博弈中的冗余路径主要指的是相同局面以不同顺序排列的路径，即换位 (transposition)。换位问题可以通过换位表解决。

Heuristic Alpha-Beta Search (启发式\(\alpha\)-\(\beta\)搜索)

极小化极大搜索不适用于枚举情况过多的博弈，即使使用\(\alpha\)-\(\beta\)剪枝和移动顺序，也无法在有限的时间内找到最优解。因此香农提出了A型和B型策略，A型策略是指在每一步决策时都考虑所有可能的移动，探索了宽而浅的部分；B型策略是指在每一步决策时都只考虑最好的几个移动，探索了窄而深的部分。

为了充分利用有限的计算资源和计算时间，使用评价函数 (evaluation function) 来代替效用函数，使用截断测试1 (cutoff test) 来代替终止状态的判断。评价函数是一种启发式函数，它可以对局面进行评估，但是它不一定能够准确地评估局面的价值。

评价函数 (Evaluation Function)

对于终止状态，评价函数必须返回准确的效用值，即\(\text{Eval}(S, P) = \text{Utility}(S, P)\)。对于非终止状态，评价函数的值必须介于输和赢之间，即\(\text{Eval}(S, P) \in [\text{Utility}(\text{loss}, P), \text{Utility}(\text{win}, P)]\)。

几种常见的评价函数：

  • 结果状态比例估计，使用结果状态的比例对其最终收益加权求和，即
\[\text{Eval}(S, P) = \sum\limits_{i=1}^{Count_{S_{T}}}\frac{Count_{S,S_{T_i}}}{\sum_{j=1}^{Count_{S_{T}}}{Count_{S,S_{T_j}}}}\text{Utility}(S_{T_i}, P)\]
  • 加权线性函数，对局面的每个特征进行加权求和2，令\(f_i(S)\)为局面\(S\)的第\(i\)个特征的价值，\(w_i\)为第\(i\)个特征的权重，则
\[\text{Eval}(S, P) = \sum\limits_{i=1}^{n}w_i f_i(S)\]

截断搜索在合适的时候停止搜索，并返回评价函数的值。

截断搜索可以与深度限制搜索结合，当遇到终止状态或达到深度限制时，返回评价函数的值。

\[\text{if IsCutoff}(S, d) \text{ then return Eval}(S, P)\]

前向剪枝 (Forward Pruning)

\(\alpha\)-\(\beta\)搜索是A型策略，考虑了同一深度所有可能的移动；而前向剪枝属于B型策略，舍弃了那些看起来就很差的移动，尽管这些移动可能会导致更好的结果；前向剪枝使用束搜索，在每一层只考虑最好的几个移动，而不是所有可能的移动。

搜索和查表 (Search and Lookup)

查表是指对已经搜索过的局面进行记录，当再次遇到相同的局面时，直接返回已知的结果。查表可以减少搜索的时间，但是会增加空间的开销。

蒙特卡洛树搜索 (Monte Carlo Tree Search, MCTS) 是一种不同于启发函数的估计方法，它使用多次完整模拟的平均最终效用来估计当前状态的价值。

随机博弈 (Stochastic Games)

  1. 随机博弈的每个开始阶段，博弈处于一种特定的状态
  2. 参与者选择某种行动，获得与之相应的奖励/收益
  3. 根据上一步的状态和行动，博弈按照某一分布转移到下一状态

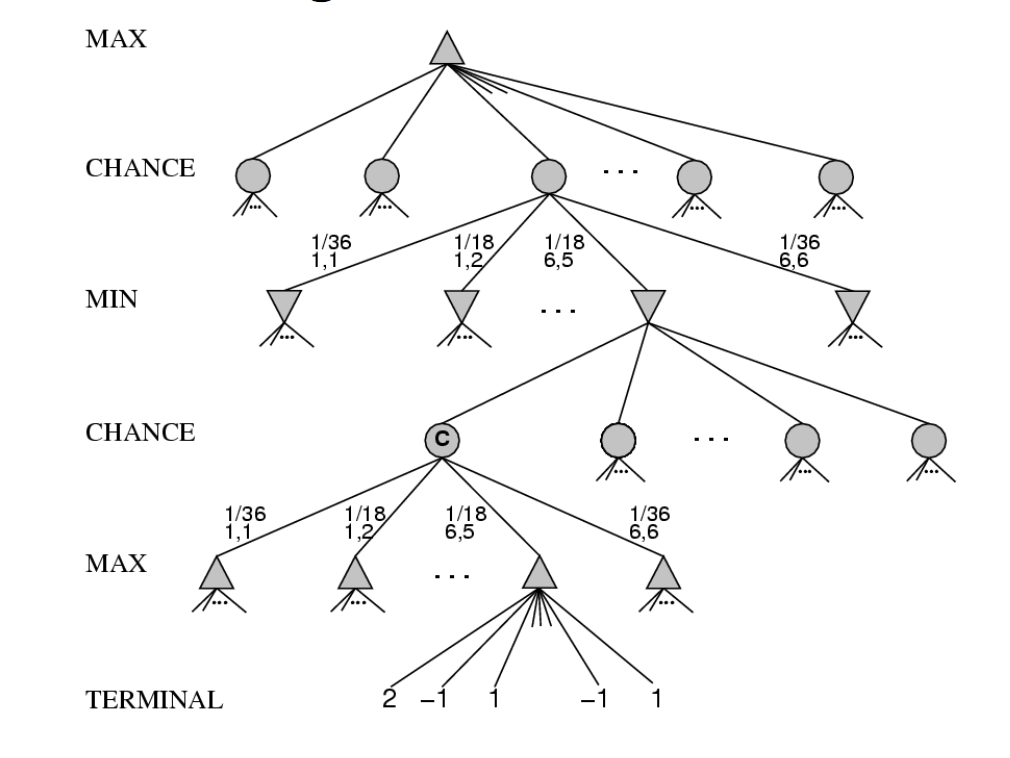
在随机博弈树中，玩家层对应的节点表示状态及最优动作，机会节点表示状态和可能的动作；从玩家层到机会层表示动作的选择，从机会层到玩家层表示状态的转移。

确定性极小极大化搜索扩展到随机博弈中变成包含机会节点的期望极小极大化搜索:

\[\text{Expected-Minimax}(S, P) = \left \{ \begin{aligned} & \text{Utility}(S, P) & \text{if IsTerminal}(S) \\ & \max\limits_{a \in Actions(S)} \text{Expected-Minimax}(\text{Result}(S, a), P) & \text{if ToMove}(S) = P \\ & \sum\limits_{s' \in S'} \text{Probability}(s' | S, a) \text{Expected-Minimax}(s', P) & \text{otherwise} \end{aligned} \right.\] 


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

 
def Expected_Minimax_Search(state) -> action:
    player = To_Move(state) # 当前玩家
    value, action = Max_Value(state, player) # 期望极小极大化搜索
    return action # 返回最优动作

def Max_Value(state, player) -> (value, action):
    if Is_Terminal(state): # 终止状态
        return Utility(state, player), None # 返回收益，动作为空
    value = -np.inf # 最大收益
    action = None # 最优动作
    for a in Actions(state): # 遍历所有可能的动作
        next_value = Expected_Value(state, a, player) # 递归调用期望极小极大化搜索
        if next_value[player] > value: # 更新更大的收益和更优的动作
            value = next_value[player] # 更新最大收益
            action = a # 更新最优动作
    return value, action # 返回最大收益和最优动作

def Expected_Value(state, action, player) -> value:
    value = 0 # 期望收益
    for next_state in Result(state, action): # 遍历所有可能的状态
        prob = Probability(state, action, next_state) # 转移到下一状态的概率
        next_player = To_Move(next_state) # 下一步的玩家
        next_value, _ = Max_Value(next_state, next_player) # 递归调用极小极大化搜索
        value += prob * next_value[player] # 更新期望收益
    return value # 返回期望收益

部分可观测博弈 (Partially Observable Games)

纳什均衡 (Nash Equilibrium) 是指在博弈中，当满足特定条件时，任何一位玩家在改变自身策略而其他玩家保持策略不变时，都不会获得更好的收益。纳什均衡是一种稳定的策略，它可以用于解决部分可观测博弈。

\[V_i(\pi_1^*, \pi_2^*, \cdots, \pi_i^*, \cdots, \pi_n^*) \geq V_i(\pi_1^*, \pi_2^*, \cdots, \pi_i, \cdots, \pi_n^*)\]

\(\alpha\)-\(\beta\)搜索使用启发函数估计价值，蒙特卡洛树搜索使用随机模拟平均价值，这两种方法都不是完美的，它们都有一定的局限性:

  1. \(\alpha\)-\(\beta\)搜索受启发函数的近似误差影响
  2. 有些时候某些动作显然是更好的，计算价值是没有必要的
  3. 两种方法都在单步移动时进行所有推理，与人类的思考方式不同

  1. 对于终止状态，截断测试必然返回真。 ↩

  2. 假设特征的贡献是独立的 ↩