Reinforcement Learning within Tree Search for Fast Macro Placement
Introduction
全局树搜索+局部策略学习:在更高层次上,蒙特卡洛树搜索(MCTS)被用来对搜索过程进行战略性导航。它利用一种新颖的滚动边界(frontier)机制,引导代理关注和利用有价值的状态,从而加强对精英解决方案的优化。下层利用 RL 代理的学习和概括能力,促进在广阔的搜索空间中进行高效探索。这种双层框架产生了一种动态协同效应:MCTS 引导的直接优化和 RL 驱动的自适应学习。
本质上是一个有记忆的搜索算法,搜索过程会记录见过的状态的最优解,并维护一个带有较优解的状态集合,在搜索过程中会不断更新这个集合,从一些优化的状态中进行搜索,而不是从头搜索,相比于每次都从头训练的方法,这种方法可以减少搜索的时间。值得一提的是这个状态集合包括树搜索中所有深度的可能的状态,或者所有时刻的可能的状态,即这些状态中已放置的macro的数量是不必一样的。作者在文中提供了理论证明,证明这种迭代方式能保证状态价值的提升,但似乎并没有证明其收敛性。从结果上来说,这个方法在HPWL上有很好的表现,与SOTA方法有一比高下的能力,但在拥塞度上没有过多说明,PPA的考量也没有给出。
Methodology
Monte Carlo Tree Search
- 树搜索是从空白画布\(s_0\)开始,在每个步骤选择一个macro,将新的状态\(s_{t+1}\)添加到孩子节点中,构建一个布局搜索树。将状态\(s\)的子结点,即放置下一个macro的新状态的集合定义为\(\mathcal{C}(s)\),经过\(s\)这一中间态得到的最终结果定义为叶子结点\(\mathcal{P}(s)\)。
- 对于节点的扩展,或者说动作的选取,采用了束搜索的方法,每次扩展时都维护一个扩展列表\(\mathcal{F}\)。
- 记录每个访问过的状态\(s\)的最优结果\(Q(s)=\max_{s_T\in \mathcal{P}(s)} -\text{HPWL}(s_T)\),并且记录访问次数\(N(s)\)。
- 状态空间是非常大的,所以必须要维护\(\mathcal{F}\)的大小,也就是滚动边界机制,参考UCT算法,定义状态\(s\)的score为\(S(s)=Q(s)+\frac{\alpha}{\sqrt{N(s)}}\),每次扩展时选择score最大的状态进行扩展。

RL
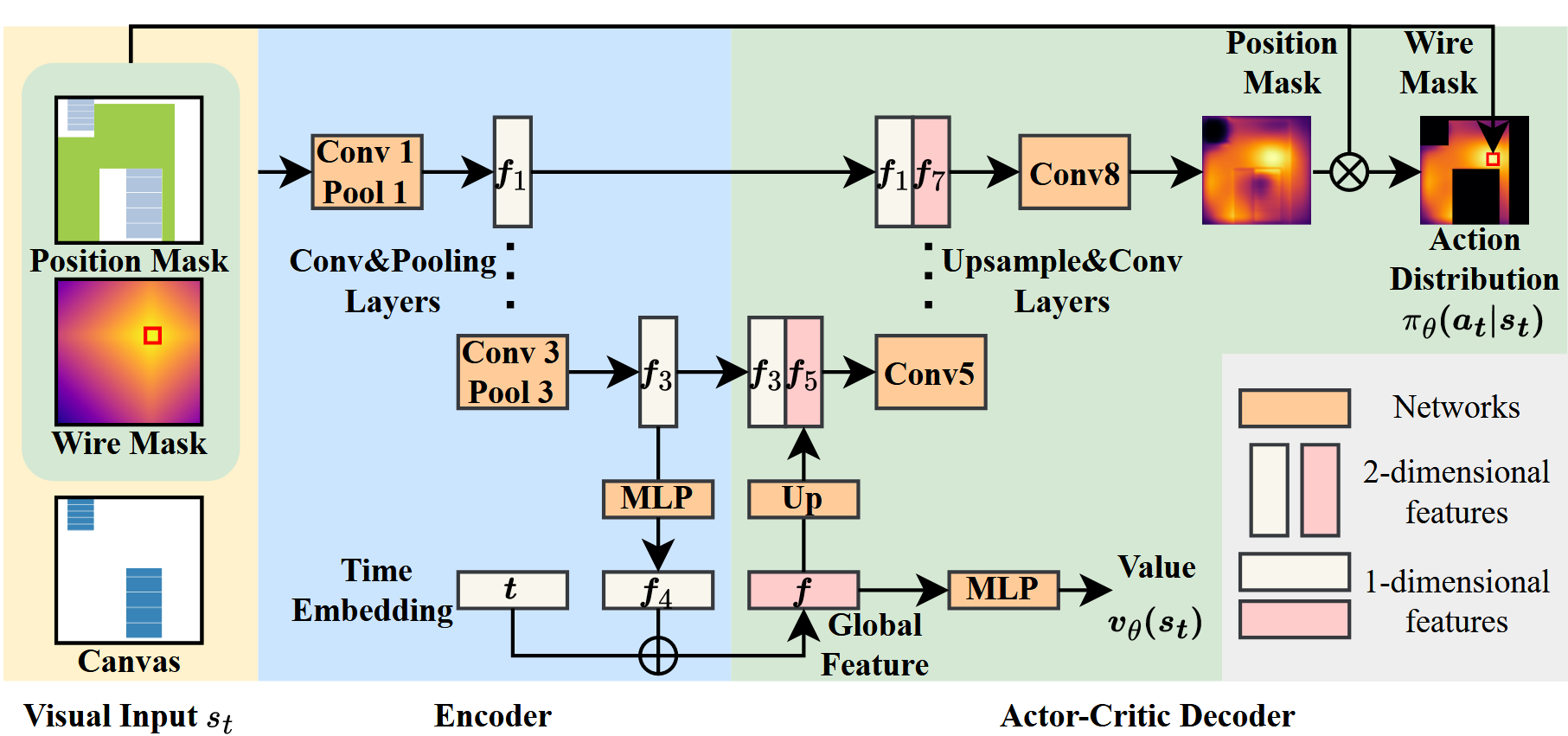
- 参考wiremask的视觉输入
- 选择线长增量最小的贪心策略
- U-net结构,actor-critic算法