Transferable Chip Placement via Offline Decision Transformer
Introduction
- offline RL
- transferable placement policy
- offline data are collected from multiple chip circuits using (near) expert-level placement behaviors, differing from the common offline RL setting where the data are collected by sub-optimal behavior policies over a single environment.
- transformer placement network
Methodology
离线强化学习的第一个要素就是离线数据的收集,这篇工作提供了12个芯片电路任务的\(500\times 12\)专家级布局结果,数据量比较大,很有研究价值。
Offline RL
给定一个轨迹\(\tau=(s_1,a_1,\dots,s_T,a_T)\),其中\(s_t\)是状态,\(a_t\)是动作,可以定义一个后视信息\(\text{HI}(\tau)\),可以理解成一个隐式可学习特征,用于指导决策,可以是任何函数,自由度较高,在一些工作中可以是累计回报,也可以是最终状态,本文是电路的可学习的embedding。本文的训练目标是最大化条件策略
\[\max_{\theta}\mathbb{E}_{(c,\tau)\sim D}\left[\sum_{t=1}^{T}\log\pi_{\theta}(a_t|\tau_t,\text{HI}(c,\tau))\right]\]其中\(D\)是经验轨迹数据集,\(c\)是电路,\(\tau_t\)是直到时间\(t\)的轨迹。
电路\(c\)可以表示为无向图\(g^c\),邻接矩阵\(A^c\in\{0,1\}^{N\times N}\),其中\(N\)是节点数,节点特征矩阵\(X^c\in\mathbb{R}^{N\times D}\),\(D\)是节点特征维度。参考VAE的思想,优化变分下界
\[\max_{\phi}\mathbb{E}_{c\sim D}\left[\mathbb{E}_{q_\phi(Z\vert X,A)}\log p(A\vert Z)-\text{KL}(q(Z\vert X,A)\Vert p(Z))\right]\]其中\(q_\phi(Z\vert X,A)=\prod_{i=1}^{N}q_\phi(z_i\vert X,A)\)是来自编码器的后验分布,\(p(A\vert Z)=\prod_{i=1}^{N}\prod_{j=1}^{N}\sigma(z_i^Tz_j)\)是来自解码器的似然分布,\(Z=\left[z_1,\dots,z_N\right]^T\)是隐变量,\(p(Z)\)是高斯先验分布。可以看出,这个模型是一个图自编码器,用于学习电路的embedding,所以用节点隐变量的均值来近似替代电路的embedding\(\text{HI}(c,\tau)=\text{HI}(c)=\frac{1}{N}\sum_{i=1}^{N}z_i\)。
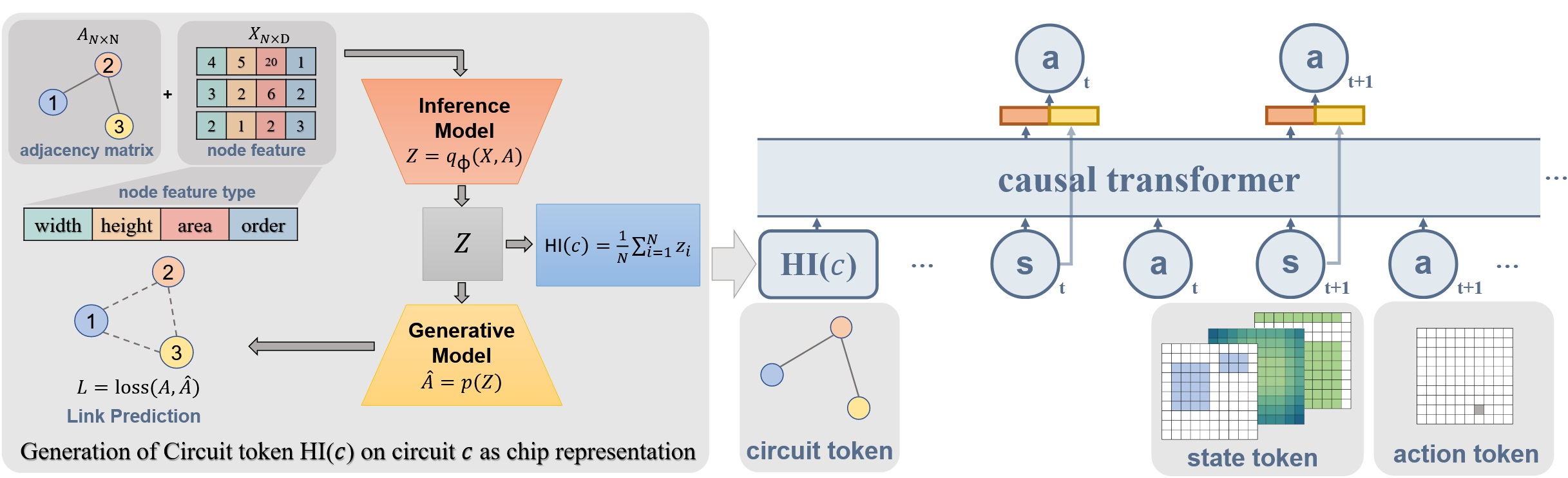
模型结构以GPT为backbone,输入包括state token和action token,以及电路的embedding,其中state token参考了MaskPlace工作,包括了position mask、wire mask和view mask三个通道,action token是二维坐标,这两个token在输入前面都有一个embedding layer进行编码。
最后是在未见电路上的微调,优化目标与条件策略是类似的,但考虑到微调时每个轮次生成的轨迹是不同的,这些轨迹可能有好有坏,所以根据轨迹的回报对其策略进行加权,此外增加了一个策略熵的正则,以增加探索性。最终的微调目标是
\[\min_\theta -\mathbb{E}_{\mathcal{B(\tau)}}\left[\omega(\tau)\log_\theta(a_t\vert \tau_t,\text{HI}(c))\right] + \lambda\max(0,\beta+\mathbb{E}_{\mathcal{B(\tau)}}[\ \log_\theta(\cdot\vert s_t,\text{HI}(c))]\]其中\(\omega(\tau)=\frac{\exp(R(\tau)/\alpha)}{\mathbb{E}_{\mathcal{B(\tau)}}\exp(R(\tau)/\alpha)}\)是轨迹的权重,\(R(\tau)\)是轨迹的回报,\(\alpha\)是温度参数,\(\beta\)是熵的最小值。