Markov Decision Process

February 28, 2024

2024   ·   RL     ·   reinforcement-learning  

Introduction

Markov Decision Process (MDP) is a mathematical framework used to model decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDP is used in reinforcement learning to model the environment and the agent’s interaction with the environment.The MDP and the agent together form a sequence of states, actions, and rewards, known as a trajectory:

\[S_0, A_0, R_1, S_1, A_1, R_2, \dots, S_T, A_T, R_{T+1}, \dots\]

Components of MDP

An MDP is defined by the following components:

  • State Space: A set of all possible states in the environment. The state space can be discrete or continuous.
  • Action Space: A set of all possible actions that the agent can take in the environment. The action space can be discrete or continuous.
  • Transition Probability: A function that defines the probability of transitioning from one state to another state given an action.
\[\begin{aligned} p(s^{\prime},r\vert s,a) &\in [0,1] \\ p(s^{\prime} \vert s,a) &= \sum_{r} p(s^{\prime},r\vert s,a) \\ \end{aligned}\\ \sum_{s^{\prime}} \sum_{r} p(s^{\prime},r\vert s,a) = 1\]
  • Reward Function: A function that defines the reward the agent receives for taking an action in a particular state.
\[\begin{aligned} r(s,a) &= \sum_{r} r \sum_{s^{\prime}} p(s^{\prime},r\vert s,a) \in \mathbb{R} \\ r(s,a,s^{\prime}) &= \sum_{r} r p(r\vert s,a,s^{\prime})= \sum_{r} r \frac{p(s^{\prime},r\vert s,a)}{p(s^{\prime}\vert s,a)} \end{aligned}\]
  • Discount Factor: A value between 0 and 1 that defines the importance of future rewards.
  • Policy: A function that defines the agent’s behavior in the environment.
  • Value Function: A function that defines the expected cumulative reward the agent can achieve from a given state.
  • Q-function: A function that defines the expected cumulative reward the agent can achieve from a given state-action pair.

Markov Reward Process

The return in MDP is defined as the sum of discounted rewards:

\[G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}\]

where \(\gamma\) is the discount factor, and \(R_{t+1}\) is the reward at time step \(t+1\), corresponding to the state-action pair \((S_t, A_t)\).

If \(\gamma = 0\), the agent is myopic and only cares about the immediate reward. If \(\gamma = 1\), the agent is far-sighted and cares about the long-term reward, but the sum may not converge.

Returns at different time steps are related as follows:

\[\begin{aligned} G_t &= R_{t+1} + \gamma(R_{t+2} + \gamma R_{t+3} + \dots) \\ &= R_{t+1} + \gamma G_{t+1} \end{aligned}\]

where time step \(t\) is not the final time step, otherwise \(G_t = R_{t+1}\). The next return of termination can be defined as \(G_{t+1} = 0\).

The bellman equation for the value function of a state is defined as follows:

\[\begin{aligned} v(s) &= \mathbb{E}[G_t \vert S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma G_{t+1} \vert S_t = s] \\ &= \mathbb{E}[R_{t+1}\vert S_t = s] + \gamma \mathbb{E}[G_{t+1} \vert S_t = s] \\ &= r(s) + \gamma \sum_{s^{\prime}} p(s^{\prime}\vert s) v(s^{\prime}) \end{aligned}\]

where \(r(s)\) is the expected reward of state \(s\), and \(p(s^{\prime}\vert s)\) is the transition probability from state \(s\) to state \(s^{\prime}\). The proof of the bellman equation is given in next section.

We can rewrite the bellman equation in matrix form:

\[V = R + \gamma P V\]

where \(V\) is the \(\vert S\vert\times 1\) vector of value function, \(R\) is the \(\vert S\vert\times 1\) vector of expected rewards, \(P\) is the \(\vert S\vert\times\vert S\vert\) transition probability matrix, where \(P_{ij} = p(s_j\vert s_i)\). The solution to the bellman equation is given by:

\[\begin{aligned} V(I - \gamma P) &= R \\ (I - \gamma P)^{-1} R &= V \end{aligned}\]

Policies and Value Functions

A policy \(\pi\) is a mapping from states to actions.

\[\begin{aligned} \pi(a\vert s) &= p(A_t = a \vert S_t = s) \\ p_{\pi}(s^{\prime}\vert s) &= \sum_{a} \pi(a\vert s) p(s^{\prime}\vert s,a) \\ r_{\pi}(s) &= \sum_{a} \pi(a\vert s) r(s,a) \\ \end{aligned}\]

The value function \(v_{\pi}(s)\) of a state \(s\) under a policy \(\pi\) is the expected return starting from state \(s\) and following policy \(\pi\):

\[v_{\pi}(s) = \mathbb{E}_{\pi}[G_t \vert S_t = s]\]

The action-value function \(q_{\pi}(s,a)\) is the expected return starting from state \(s\), taking action \(a\), and then following policy \(\pi\):

\[q_{\pi}(s,a) = \mathbb{E}_{\pi}[G_t \vert S_t = s, A_t = a]\]

Both value functions can be defined recursively in terms of each other:

  • For state-value function:
\[\begin{aligned} v_{\pi}(s) &= \mathbb{E}_{\pi}[G_t \vert S_t = s] \\ &= \mathbb{E}_{\pi}[R_{t+1} + \gamma G_{t+1} \vert S_t = s] \\ &= \sum_{a} \pi(a\vert s) \sum_{s^{\prime},r} p(s^{\prime},r\vert s,a) [r + \gamma \mathbb{E}_{\pi}[G_{t+1} \vert S_{t+1} = s^{\prime}]] \\ &= \sum_{a} \pi(a\vert s) \sum_{s^{\prime},r} p(s^{\prime},r\vert s,a) [r + \gamma v_{\pi}(s^{\prime})]\\ &=\sum_a \pi(a\vert s) \sum_r r \sum_{s^{\prime}} p(s^{\prime},r\vert s,a) + \gamma \sum_{s^{\prime}} p(s^{\prime}\vert s,a) v_{\pi}(s^{\prime})\\ &= r_{\pi}(s) + \gamma \sum_{s^{\prime}} p_{\pi}(s^{\prime}\vert s) v_{\pi}(s^{\prime}) \end{aligned}\]
  • For action-value function:
\[\begin{aligned} q_{\pi}(s,a) &= \mathbb{E}_{\pi}[G_t \vert S_t = s, A_t = a] \\ &= \mathbb{E}_{\pi}[R_{t+1} + \gamma G_{t+1} \vert S_t = s, A_t = a] \\ &= \sum_{s^{\prime},r} p(s^{\prime},r\vert s,a) [r + \gamma \mathbb{E}_{\pi}[G_{t+1} \vert S_{t+1} = s^{\prime}]] \\ &= \sum_{s^{\prime},r} p(s^{\prime},r\vert s,a) [r + \gamma v_{\pi}(s^{\prime})] \\ &=\sum_r r \sum_{s^{\prime}} p(s^{\prime},r\vert s,a) + \gamma \sum_{s^{\prime}} p(s^{\prime}\vert s,a) v_{\pi}(s^{\prime})\\ &= r(s,a) + \gamma \sum_{s^{\prime}} p(s^{\prime}\vert s,a) v_{\pi}(s^{\prime}) \end{aligned}\]
  • Relation between value functions:
\[\begin{aligned} v_{\pi}(s) &= \sum_{a} \pi(a\vert s) q_{\pi}(s,a) \\ q_{\pi}(s,a) &= \sum_{s^{\prime},r} p(s^{\prime},r\vert s,a) [r + \gamma \sum_{a^{\prime}} \pi(a^{\prime}\vert s^{\prime}) q_{\pi}(s^{\prime},a^{\prime})]\\ &= r(s,a) + \gamma \sum_{s^{\prime}} p(s^{\prime}\vert s,a) \sum_{a^{\prime}} \pi(a^{\prime}\vert s^{\prime}) q_{\pi}(s^{\prime},a^{\prime}) \end{aligned}\]

Backup Diagrams

Backup diagrams are a tree-like representation of the recursive nature of the value functions. The root of the tree represents the current state, leaf nodes of the state-node represent the possible actions, and the leaf nodes of the action-node represent the possible next states. Edges from state-node to action-node represent the policy \(\pi(a\vert s)\), and edges from action-node to state-node represent the transition probability \(p(s^{\prime}\vert s,a)\).

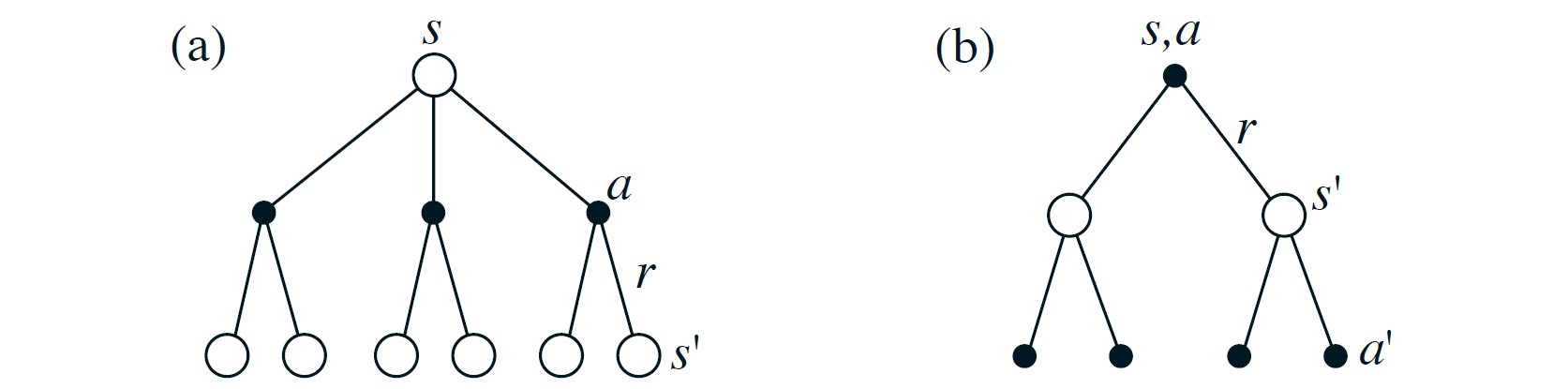
Bellman optimality equation

The optimal value functions satisfy the following bellman optimality equation:

\[\begin{aligned} v^{\ast}(s) &= \max_{a} q^{\ast}(s,a) \\ q^{\ast}(s,a) &= \mathbb{E}[R_{t+1} + \gamma v^{\ast}(S_{t+1}) \vert S_t = s, A_t = a] \\ &= r(s,a) + \gamma \sum_{s^{\prime}} p(s^{\prime}\vert s,a) v^{\ast}(s^{\prime}) \end{aligned}\]

which means that the optimal value function of a state is the maximum action-value function over all actions, and the optimal action-value function of a state-action pair is the expected reward of the state-action pair plus the maximum value function of the next state.

The optimal policy can be obtained from the optimal action-value function:

\[\pi^{\ast}(a\vert s) = \begin{cases} 1 & \text{if } a = \arg\max_{a} q^{\ast}(s,a) \\ 0 & \text{otherwise} \end{cases}\]

When it comes to the iterative realtionship between the optimal value functions and themselves:

\[\begin{aligned} v^{\ast}(s) &= \max_{a} q^{\ast}(s,a) \\ &= \max_{a} [r(s,a) + \gamma \sum_{s^{\prime}} p(s^{\prime}\vert s,a) v^{\ast}(s^{\prime})] \\ q^{\ast}(s,a) &= \mathbb{E}[R_{t+1} + \gamma v^{\ast}(S_{t+1}) \vert S_t = s, A_t = a] \\ &= \mathbb{E}[R_{t+1} + \gamma \max_{a^{\prime}} q^{\ast}(S_{t+1},a^{\prime}) \vert S_t = s, A_t = a] \\ &= r(s,a) + \gamma \sum_{s^{\prime}} p(s^{\prime}\vert s,a) \max_{a^{\prime}} q^{\ast}(s^{\prime},a^{\prime}) \\ &=\sum_{s^{\prime},r} p(s^{\prime},r\vert s,a) [r + \gamma \max_{a^{\prime}} q^{\ast}(s^{\prime},a^{\prime})] \end{aligned}\]